Vamos agora estudar a Teoria de Relatividade Especial, proposta por Albert Einstein em 1905.
Mas o que a Relatividade tem a ver com Matéria e Radiação? A Teoria da Relatividade descreve objetos, cujas velocidades são muito elevadas, comparáveis à maior possível, a velocidade da luz no vácuo. As partículas subatômicas são os objetos que conseguem ter essas velocidades extremas. Essa Teoria também apresentou a relação entre massa e energia, a famosa equação E=mc2, mostrando que as minúsculas massas dos átomos podem gerar uma enorme quantidade de energia.
Não podemos usar o nosso senso comum para entender a Relatividade!
No nosso mundinho lento e Newtoniano, quando estamos viajando num automóvel a 100 km/h, numa rodovia de mão dupla, sabemos do perigo de ocorrer uma colisão frontal com outro veículo vindo em sentido oposto a 100 km/h na nossa direção. A velocidade relativa do outro veículo, em relação ao nosso, neste caso é de 200 km/h.
Se fôssemos um quantum e estivéssemos viajando na velocidade c da luz, veríamos outro quantum vindo no sentido oposto com que velocidade?
Com 2c, como no nosso mundinho Newtoniano?
Não! De acordo com a Relatividade, a luz possui a mesma volocidade c
em todos os sistemas de referência inerciais.
Alguém então diria: "Isto está errado, meu senso comum me diz que não é
assim!"
Mas quem dá o veredito para uma teoria da Física são os resultados de
experiências que verificam as suas previsões, e estes confirmam a
teoria
de Albert Einstein. Logo, ela está correta.
As previsões da Relatividade são mensuráveis somente para velocidades
comparáveis à velocidade da luz. Para corpos com velocidades muito
menores do que a velocidade da luz, as equações das duas teorias são
equivalentes.
Em 1860, James
C. Maxwell unificou as leis empíricas da eletricidade e do
magnetismo nas suas quatro equações
do eletromagnetismo clássico. Esta descoberta levou-o a
prever que a luz é uma onda eletromagnética e a sua velocidade no vácuo
é dada por
onde são as constantes elétrica e
magnética do vácuo.
Estas equações colocaram novos problemas para os físicos, pois não são
invariantes à transformação de Galileu, fazendo com que a força
eletromagnética tenha formas diferentes, dependendo do referencial
inercial utilizado para o seu cálculo. Outra questão em aberto era qual
o meio em que estas ondas viajavam. Na época, foi sugerida a existência
de um éter com estranhas propriedades como meio de propagação
das ondas eletromagnéticas. 
Entretanto nenhuma experiência conseguiu comprovar a existência deste éter. Foi o maravilhoso experimento de Michelson-Morley que colocou em xeque a existência do éter, pois Michelson projetou um aparato genial e preciso, mas não conseguiu comprová-la. Acredito que podemos dizer que foi a medição frustrada de maior sucesso. Michelson foi agraciado em 1907 com o prêmio Nobel.
Em 1905, com 26 anos, Albert Einstein
publicou quatro artigos fundamentais para a Física Moderna. Com o
trabalho do efeito fotoelétrico, ele foi agraciado com o Prêmio Nobel,
mas a sua enorme fama ocorreu após a comprovação da sua Teoria da
Relatividade Especial.
Os dois Postulados da Relatividade Especial enunciados por Einstein são:
Postulado 1 - As leis da Física são as mesmas em todos os referenciais inerciais. Não existe um referencial absoluto.
Postulado 2 - A velocidade da luz no vácuo tem o
mesmo valor c em todas as direções e em todos os referenciais
inerciais. 
O primeiro postulado é uma extensão do Princípio da Relatividade de
Newton, agora enunciado para todos os fenômenos físicos e não somente
para a mecânica.
Uma importante consequência do segundo postulado é que a velocidade da luz é a mesma para todos os observadores, independentemente da velocidade relativa entre o observador e a fonte. As consequências deste postulado foram enormes, mudou radicalmente os conceitos de espaço e tempo, e unificou a energia e a massa.
Vamos agora para mais uma seção do nosso cineminha!
Assista neste vídeo a explicações sobre o abandono da ideia do éter e sobre o segundo postulado de Einstein para a Teoria da Relatividade Especial, que afirma que a velocidade da luz é uma grandeza invariante, isto é, tem o mesmo valor em todos os referenciais inerciais. Você verá também que o tempo é relativo e depende do referencial inercial. No final do vídeo, é apresentada uma comprovação da dilatação do tempo, através da chegada à superfície terrestre de múons gerados na alta atmosfera.
Bom divertimento!
Os Postulados de Einstein levam à
relatividade da simultaneidade, que podemos descrever assim:
Dois eventos em um referencial inercial são simultâneos, se os sinais luminosos associados a eles forem detectados simultaneamente por um observador situado em um ponto equidistante dos dois eventos.
Agora vamos utilizar o desenho animado (clique na figura) de uma situação proposta por Einstein para mostrar a relatividade da simultaneidade. Você encontrará mais explicações durante a execução deste desenho animado. Durante a apresentação da animação, utilize os botões de controle para parar, continuar e mostrar passo a passo a evolução do movimento.
Qual a sua conclusão sobre eventos simultâneos em referenciais inerciais com movimento relativo entre eles?
Vamos ver agora
algumas questões importantes para a compreensão da Teoria da
Relatividade Especial, que abreviarei como TRE, e o enunciado dos seus
dois postulados.
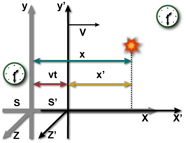
Na Relatividade, utilizamos um sistema de coordenadas, para medir distâncias entre pontos no espaço, e um sistema de relógios, para medir os instantes de tempo para cada sistema inercial.
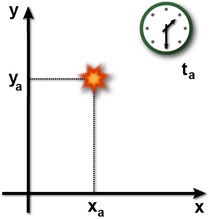Um evento, por
exemplo, evento A, é um acontecimento ao qual um observador em um
referencial inercial pode atribuir coordenadas espaciais (xA,yA,zA)
e uma coordenada temporal tA. Um evento é algo que acontece,
como uma porta que se abre, uma estrela que explode, uma luz que se
acende, duas partículas que se chocam.
Todo evento ocorre num determinado ponto do espaço e num determinado tempo, mas os eventos não dependem do referencial inercial utilizado para descrevê-lo.
Vamos ver agora outra novidade trazida pelo
segundo postulado da Relatividade: a dilatação do tempo.
Nesta animação gráfica (clique na figura), temos dois referenciais inerciais - um em repouso e o outro em movimento. Comparando as distâncias percorridas pela luz, para um intervalo de ida e volta entre dois espelhos, concluímos que o intervalo de tempo medido pelo relógio do referencial em movimento é maior do que o do relógio do referencial em repouso, isto é, existe uma dilatação do tempo. Ou, em outras palavras, o relógio do referencial em movimento é mais lento. Note que este resultado é alcançado porque a velocidade da luz é a mesma nos dois sistemas de referência.
Complete o cálculo iniciado na animação gráfica e obtenha a equação da dilatação do tempo
O intervalo de tempo entre eventos que ocorrem no mesmo local, num determinado referencial, é denominado de tempo próprio, Δtp.
Utilize agora esta outra simulação gráfica (clique na figura) para fixar o conceito da relatividade do tempo. Boa viagem!
Acabamos de ver que o relógio do
referencial em movimento anda mais devagar, dilatando o tempo. Agora
veremos o que acontece com a distância neste mesmo referencial em
movimento.
O comprimento de um corpo medido no referencial em que ele está em repouso é denominado de comprimento próprio, ΔLp.
Nesta animação gráfica (clique na figura), é utilizado um relógio
que se move com velocidade v em relação ao sistema de referência em
repouso. O comprimento próprio é medido utilizando-se a velocidade v
e o intervalo de tempo do referencial em movimento, ΔLp=v
Δt.
Como o movimento visto pelo referencial do relógio, agora ele está parado numa posição e temos o tempo próprio, então podemos escrever: ΔL=v Δtp.
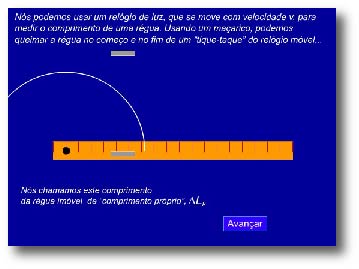Complete os cálculos e chegue na
equação da contração dos comprimentos
Atenção, as outras dimensões (Δy e Δz) não mudam, pois são perpendiculares ao movimento relativo que ocorre no eixo x.