Estudaremos a dilatação do tempo de vida dos múons na atmosfera terrestre e a contração do comprimento do seu percurso.
Veremos que a abundância das partículas múons na superfície da Terra só pode ser explicada com o uso das equações relativísticas.
Inicialmente, vamos conhecer a origem dessas partículas relativísticas, como e onde são produzidas e quais são as suas características principais.
Após conhecermos um pouco destas partículas, realizaremos um cálculo da
previsão de alcançarem a superfície da Terra, após serem produzidas na
alta atmosfera. As previsões obtidas com a mecânica clássica e com as
equações da Teoria da Relatividade Especial serão comparadas.
Você sabia que somos atravessados ininterruptamente por estas partículas?
Mas pode ficar tranquilo!
Isto ocorre desde a formação do Universo, antes mesmo de o homem existir.
 |
| (Clique na imagem
para ampliá-la ) |
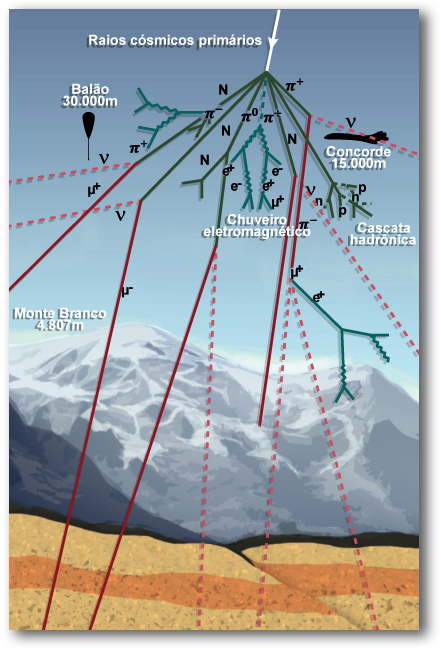
Continuamente, raios cósmicos de alta energia, vindos do espaço sideral, entram na atmosfera terrestre e interagem com seus elementos, dando assim início a um processo de produção de partículas em cascata, que dá origem a milhares de partículas secundárias.
A partícula múon foi descoberta em 1937 por J. C. Street e E. C. Stevenson, e simultaneamente por a Carl D. Anderson e Seth Neddermeyer, através de experimentos utilizando a radiação cósmica.
Inicialmente, acreditou-se que o múon fosse a partícula prevista por Yukawa em 1935, mas a descoberta do píon em 1947, pelo grupo de Bristol, com participação decisiva do físico brasileiro Cesar Lattes, mostrou ser esta última a partícula prevista pela teoria de Yukawa.
Os múons não sentem a interação forte do núcleo atômico e na sua trajetória perdem energia por ionização até decaírem. Isto faz com que a sua trajetória seja retilínea.
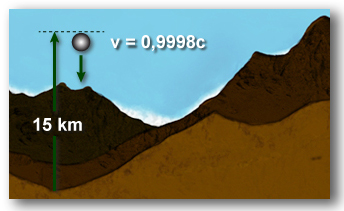
A maior parte dos múons é criada a uma altitude de 15 km, possuindo uma velocidade de 0,9998c (c = velocidade da luz no vácuo). Esta alta velocidade faz com que o seu tempo de vida no sistema de referência do laboratório seja consideravelmente dilatado.
Os múons decaem de acordo com a lei
estatística da radioatividade
onde N(t) é o número de múons no instante t, No o número de múons no tempo t=0 e τ o seu tempo médio de vida.
Agora vamos utilizar a mecânica clássica para descrever a viagem do múon desde o seu ponto de produção, 15 km acima do nível do mar, até a superfície da Terra.
O tempo que os múons levam para percorrer 15 km de atmosfera visto no referencial da Terra é dado por
Então o número N de múons que chegam ao nível do mar em relação ao número No de múons produzidos a 15 km de altitude é dado por
A previsão feita com a mecânica clássica é de que somente 132 de cada trilhão de múons produzidos chegam à superfície. Praticamente nenhum!
Acabamos de ver que o tratamento clássico da
viagem do múon não explica a sua abundante presença na superfície
terrestre. Então, vamos ver o que prevê a Teoria da Relatividade
Especial.
A equação da dilatação do tempo, com o tempo próprio do múon τ, fica
Utilizando este valor de tempo dilatado na equação do decaimento, temos
A previsão de chegada dos múons na superfície terrestre, obtida através da Teoria da Relatividade Especial, é 4.800.000.000 (quatro trilhões, oitocentos bilhões) de vezes maior do que a previsão não relativística, estando em acordo com os resultados experimentais.
O resultado equivalente pode ser obtido, se analisarmos o movimento a partir do referencial do múon.
Neste caso, devemos utilizar a equação da contração da distância. Observe que ΔLp é a distância do ponto de produção do múon na atmosfera ao solo terrestre, medida no referencial da Terra.
Podemos agora calcular a taxa de múons sobreviventes na superfície terrestre
Como esperado, o resultado é o mesmo do cálculo com a equação da dilatação do tempo, reafirmando a validade da Teoria de Relatividade Especial.