
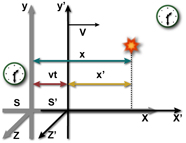

Veremos agora as equações que transformam um evento (x,y,z,t) de um sistema inercial para o outro. Serão apresentadas as transformações de Galileu, utilizadas na mecânica clássica, e as transformações de Lorentz, empregadas na Teoria da Relatividade Especial. Hendrik Antoon Lorentz publicou essas transformações antes de Einstein, mas não fez a interpretação física expressa nos postulados da TRE.
Por simplicidade, a velocidade v do referencial S' é paralela ao eixo x.
 |

|
 |
|
|
|
As equações inversas para S'→S são simétricas. Para obtê-las, basta trocar v por -v e permutar as variáveis com apóstrofo pelas sem apóstrofo:
Vamos agora encontrar as equações da transformação de Lorentz para as velocidades, considerando um corpo movendo-se no referencial S', com velocidade U' paralela ao eixo x' (U'=u'x)
A velocidade é dada pela derivada temporal da posição, logo, utilizando as equações da transformação de Lorentz, podemos escrever:
Então a equação da transformação S→S' da velocidade fica:
Para obter a transformação de S'→S, troque v por -v e u'x por ux
Se uma partícula se move com velocidade +0,80c em relação a um
referencial e uma outra partícula se move com velocidade -0,90c
em relação a este mesmo referencial, então a velocidade da segunda
partícula, vista no referencial da primeira partícula, será: 

Agora, podemos calcular a velocidade relativa de uma colisão frontal de dois automóveis, viajando a 100 km/h, e a de dois quanta, viajando à velocidade c da luz.
Agora que já vimos um pouco das novidades da cinemática relativística, vamos estudar as mudanças geradas pela TRE na dinâmica. Em particular, vamos ver como ficaram o momento linear p, a massa e a energia de uma partícula relativística.
Na mecânica clássica, o vetor momento linear p de uma partícula é definido como o produto da massa pelo vetor velocidade, p=mu. Num sistema de partículas isolado, o momento total do sistema permanece constante. A conservação do momento linear do sistema isolado é utilizada na solução de problemas de colisões, decaimentos e explosões, entre outros. Mas, se usarmos esta definição clássica para o momento linear, podemos mostrar que o momento total do sistema é conservado no referencial inercial S. Mas, quando usamos as equações da transformação de Lorentz, o momento total não é conservado no referencial S'.
A nova definição de momento linear, que sempre satisfaz a conservação do momento e torna-se equivalente à definição clássica para velocidades muito menores do que c, é dada por:
onde mo é a massa do corpo medida no referencial em repouso, denominada de massa de repouso.
O gráfico abaixo mostra o módulo do momento relativístico e o do
clássico. Note que a diferença
entre eles começa a ser acentuada somente para valores acima de 0,6c.
Para encontrar a expressão para a energia cinética relativística, vamos utilizar o Teorema do trabalho-energia, W=ΔK, com a nova definição de momento linear relativístico. Vamos considerar que a força e o movimento estão somente no eixo x.
Com a nova definição relativística de momento, podemos escrever ,
que, quando levada à equação acima, junto com
, e
assumindo que o corpo sai do repouso até a velocidade u, é reescrita
como:
 |
| (Clique na imagem para ampliá-la) |
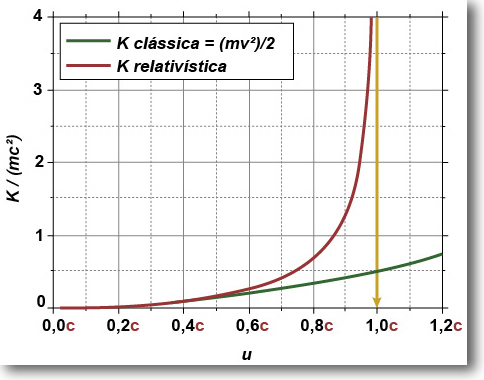
Logo, a expressão para a energia cinética relativística é
O primeiro termo depende da velocidade u, já o segundo não depende e é denominado energia de repouso, Eo=moc2. Você pode ver outras deduções desta equação clicando aqui.
A equação de energia cinética relativística mostra que uma partícula com massa de repouso não nula só pode ter velocidades no vácuo inferiores a c.
É bom lembrar que a luz num meio transparente viaja com velocidade menor do que c, Vluz no meio=c/n. Nesses meios transparentes, partículas (elétrons, prótons, múons e outras) podem superar a velocidade da luz no meio em questão.

Vendo o gráfico desta função linear junto com E=mgh, com h=100 metros (clique no gráfico), você tem uma ideia da grandeza desta descoberta.
(Clique na imagem para ampliá-la)
A energia relativística total ET é definida como a soma da energia cinética K com a energia de repouso
Sabendo que a massa de repouso do elétron é mo=0,511 MeV/c2, e que este possui uma velocidade u=0,85c, calcule a sua energia total ET, a sua energia cinética K e o seu momento linear p. Expresse os resultados em MeV e MeV/c.
Uma nave espacial passa por um observador, com velocidade v=0,8c na direção x. Quando em repouso, a altura e o comprimento da nave são: y=5 m e x=5 m. Quais os valores da altura e do comprimento vistos pelo observador em repouso?

| a) |
| b) |
| c) |
| d) |

| a) |
| b) |
| c) |
Revistas/Artigos
Vídeos
Livros